Modified Cam-Clay Model (MCC)
The Modified Cam-clay model was originally designed to describe plastic straining of clayey soils found in the state of triaxial compression. The basic assumption is that regardless of their point of departure all material points moving along a certain stress path with a progressively evolving yield surface eventually end at a unique critical void ratio line that belongs to a unique limit state surface (SBS) in the J - σm - e space, where e is the void ratio, σm is the mean stress and J is the equivalent deviatoric measure of deviatoric stress components. Assuming J = 0 allows us to project all points inside the yield surface in to the space bounded by σm - e axes and by the normal consolidation line (isotropic NCL). This line corresponds to the highest void ratio associated with a give mean stress. A graphical representation is evident from the following figure, where e0 represents the maximum void ratio associated with ![]() .
.
From the modeling point of view it is it appears more convenient to replace the σm - e space with the σm - εv space. The stiffness parameters κ, λ and κ*, λ* are related by
![]()
where ein represents the initial void ratio and for a given initial stress state it is provided by, see the figure below,
![]()
Further details can be found in the theoretical manual.
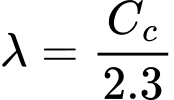 Response in the case of isotropic compression: a) σm - e space, b) σm - εv space, c) initial stress state
Response in the case of isotropic compression: a) σm - e space, b) σm - εv space, c) initial stress state
Considering a virgin (normally consolidated) soil the soil behavior is described by the normal consolidation line (NCL). Providing the soil was already consolidated to a certain stress level given by the preconsolidation pressure pc followed by unloading the material point initially moves during subsequent reloading along the swelling line (unloading-reloading). Once exceeding the parameter pc the soil behavior is again driven by the normal consolidation line (primary loading - compression line).
The nonlinear evolution of pc is given by
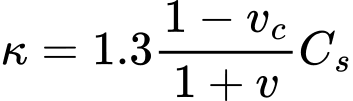
where Δεvpl the increment of volumetric plastic strain. The theoretical formulation assumes an associated plastic flow. The evolution of plastic strains thus depends on the shape of yield surface plotted in the following figure suggesting, similarly to the Drucker-Prager model, a circular projection into the deviatoric plane. As evident from its projection into the meridian plane, the preconsolidation pressure pc tends to either increase, the material hardens (normally consolidated or lightly overconsolidated soil), or decrease, the material undergoes softening (highly overconsolidated soils) until arriving at a critical state. The mathematical description of the process of hardening/softening is provided in the theoretical manual. It is worth mentioning that the predicted degree of softening may considerably exceed the degree of softening observed for real soils. Moreover, the model considerably overestimates the shear strength of overconsolidated soils. These drawbacks are partially solved in the formulation of the Generalized Cam-clay model or the Soft soil model.
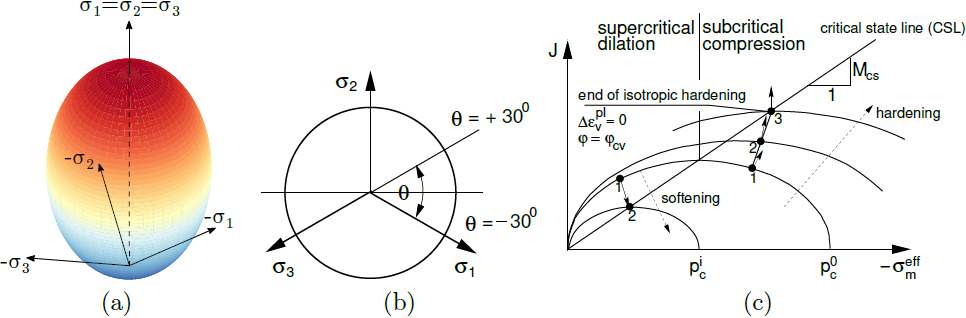 a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
Parameters defining the Modified Cam-clay material model are summarized in the following table.
Symbol | Units | Description | |
| [-] | Slope of swelling line | |
| [-] | Slope of normal consolidated line | |
| [-] | Maximum void ratio on | |
| [-] | Poisson's ratio | |
| [-] | Slope of critical state line (can be expressed in terms of | |
| [kN/m3] | Bulk weight | |
| [-] | Overconsolidation ratio | |
| [kPa] | Preoverburden pressure | |
| [1/°] | Coefficient of thermal expansion (when considering temperature effects) | |
| [°] | Critical state friction angle (not inputted) | |
| [kPa] | Preconsolidation pressure |
The slope of critical state line Mcs can be expressed in terms of the critical state friction angle φcs. The current implementation assumes the state of triaxial compression
![]()
The stiffness parameters can be estimated as
![]()
where Cc is the one-dimensional compression index and Cs is the swelling index. These parameters can be obtained from a simple oedomteric test. Further details are provided here. However, should the measurements from simple laboratory tests be available, it is more convenient to calibrate the model parameters employing for example the calibration software ExCalibre.
Point out that the modulus of elasticity E is not one of the input parameters, but instead it is determined from the bulk modulus Ks and Poisson's ratio. Point out that the bulk modulus is not constant and can be expressed in terms of the current value of mean effective stress as
![]()
where Ksmin is the minimum value of this parameter. Cleary, for very small stresses this value is rather small and therefore it is necessary, for example when modeling simple laboratory tests, to choose a sufficiently small initial load step. To speed up convergence it appears useful to exploit the Minimum number of iterations for a single load step. The influence of magnitude of the initial load step on the evolution of stress and strain is described in detail here.
From the above discussion it becomes clear that setting the initial preconsolidation pressure pcin and the initial bulk modulus Kin requires considerable attention. Both parameters are set in dependence on the current state of stress at the time the Modified Cam-clay model is introduced into the analysis. The preconsoliadtion pressure pcin is determined such that the current stress state satisfies the yield function. Details can be found here. If we limit our attention to the determination of initial geostatic stress, in which case the model is assumed to enter the analysis already in the first calculation stage, the program offers three options:
K0 procedure
In the case of ![]() procedure the initial mean stress for normally consolidated soils follows from
procedure the initial mean stress for normally consolidated soils follows from
![]()
where K0NC is the corresponding coefficient of lateral earth pressure at rest and h is the vertical distance from the terrain surface. The associated value of pcin can be further adjusted based on the current degree of overconsolidation. Point out that this is the only option how to introduce the state of overconsolidation in the analysis using parameters OCR and POP. Further details can be found here.
Elastic analysis
Recall that the program allows for replacing soils between individual calculation stages. This option can be exploited in cases when the K0 procedure cannot be used. The initial mean stress is then determined on the basis of elastic analysis. From the second stage on the elastic model is replaced by the required Modified Cam-clay model. The effect of overconsolidation must be introduced computationally.
Plastic analysis
Plastic analysis assumes application of the Modified Cam-clay model already in the first calculation stage. In such a case the material point is assumed to move down the normal consolidation line with the initial values of pcin = 1 KPa and Kin = 1/κ*. The effect of overconsolidation must be introduced computationally.
Providing the undrained conditions are required in the analysis one may proceed with the Type (1): analysis in effective stress (cef, φe) only.
The Modified Cam-clay model also allows for performing the stability analysis. However, this option is available only when running the stability analysis analysis within a given construction stage. In this case the reduction procedure adjusts the slope of critical state line Mcs in dependence on the reduced value of the critical friction angle φcs as follows
![]()
where ζ is the reduction coefficient, φcs is the actual value of the critical state friction angle determined on the basis of the inputted value of Mcs and φcs, d is the reduced value. The Factor of safety FS is then given by
![]()
The bulk modulus is kept fixed during the reduction process. It is set equal to the one at the and of the corresponding stress analysis in a given calculation stage.
Implementation of the Modified Cam-clay material model into the GEO5 FEM program is described in detail in the theoretical manual.