Eigenvalue analysis - calculation of eigenfrequencies and eigenmodes
Eigenvalue analysis provides the N lowest eigenfrequencies and eigenmodes of the system. This number is specified by the user. The resulting frequencies are primarily used to calculate the parameters of the "Rayleigh damping".
The analysis is carried out employing the inverse subspace iteration method. There are two options allowing for choosing either the Gram Schmidt orthogonalization method or the Jacobi method.
The Jacobi method typically requires less number of iterations and the number of found frequencies is typically higher than the number set by the user. It may, however, happen that some frequencies are during the search omitted. To check this, the program adopts the Sturm sequence.
The Gram Schmidt method is computationally more demanding but more reliable in finding all the desired frequencies.
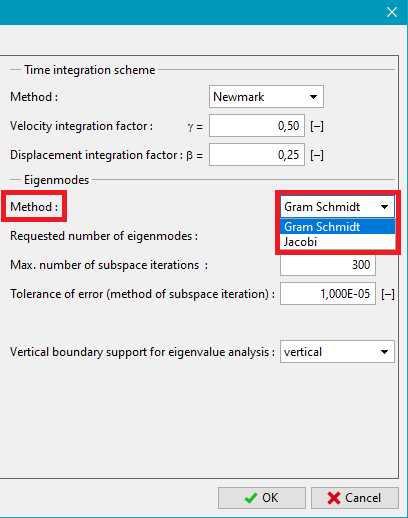Methods for Eigenvalue analysis
When choosing eigenfrequencies for the calculation of parameters of material damping it is often necessary to select a suitable mode shape corresponding to the prescribed load - purely horizontal vibration mode (only the horizontal component of the acceleration vector is introduced), or purely vertical vibration mode (only the vertical component of the acceleration vector is introduced), or the combination of both modes (both components are prescribed). Eliminating some of the modes might be therefore desirable and can be achieved by selecting suitable kinematic boundary conditions on lateral boundaries of the numerical model.
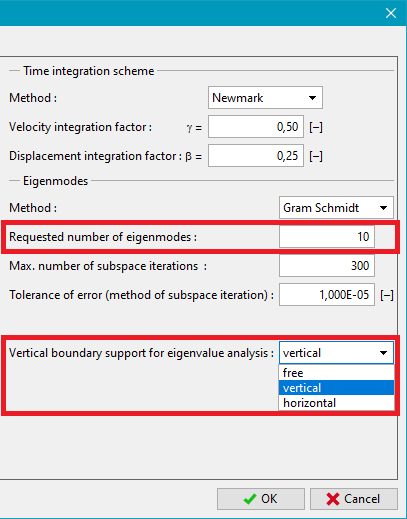Boundary conditions on vertical boundaries for Eigenvalue analysis
The program allows for the following variants of kinematic boundary conditions:
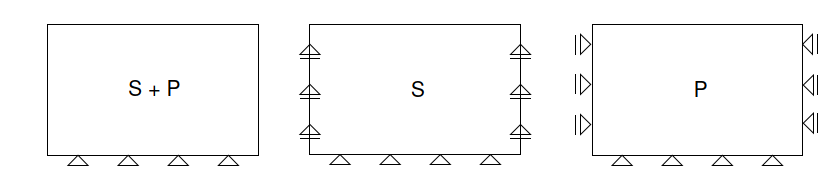Vertical support type available for Eigenvalue analysis
An additional hint for selecting the desired modes shape for the calculation of parameters of material damping are the "Modal participation factor" Γα,i and "Modal effective mass" mα,i representing participation of a given eigenmode in either horizontal or vertical component of the vibration.
Further details are available in the theoretical manual on our website.