Modifikovaný Mohr-Coulomb (MMC)
Modifikovaný Mohr-Coulombův model představuje určité rozšíření Mohr-Coulombova modelu. Plocha plasticity je podobně jako v případě smykové plochy plasticity Soft soil modelu, případně limitní plochy plasticity Hardening soil modelu, definovaná pomocí Matsuoka-Nakai podmínky porušení. Grafické znázornění funkce plasticity je patrné z následujícího obrázku. Z průmětu plochy plasticity do deviatorické roviny je zřejmé, že s klesajícím úhlem vnitřního tření φ se podmínka plasticity blíží Drucker-Pragerovu modelu, zatímco pro vyšší hodnoty φ se blíží Rankinově podmínce plasticity.
Na rozdíl od Drucker-Pragerova modelu však směrnice průmětu do meridiální roviny Mφθ není konstantní, ale závisí na hodnotě Lodeova úhlu (Mφθ = Mφθ(φ, θ)). V každém případě je podmínka plasticity Modifikovaného Mohr-Coulombova modelu konvexní hladká křivka a protíná všechny vrcholy Mohr-Coulombova modelu. Naproti tomu funkce plastického potenciálu, která řídí vývoj plastických přetvoření, je totožná s plastickým potenciálem Drucker-Pragerova modelu. Je tudíž nezávislá na Lodeovu úhlu. Je tedy závislá pouze na hodnotě úhlu dilatance ψ (Mψ = Mψ(ψ)). Obecně platí, že φ ≠ ψ, což odpovídá neasociovanému zákonu plastického tečení.
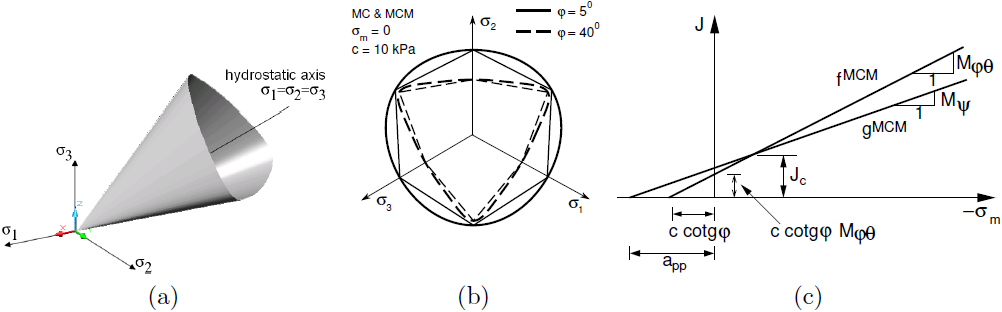 a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
Na rozdíl od všech ostatních modelů, ať již elastických-perfektně plastických nebo elasto-plastických se zpevněním/změkčením, umožňuje Modifikovaný Mohr-Coulombův model vývoj plochy plasticity v závislosti na vývoji ekvivalentního deviatorického plastického přetvoření Edpl. Konkrétně jsou definovány funkce vývoje parametrů smykové pevnosti c(Edpl) a φ(Edpl). Předpokládaná, po částech lineární, závislost je patrná z obrázku.
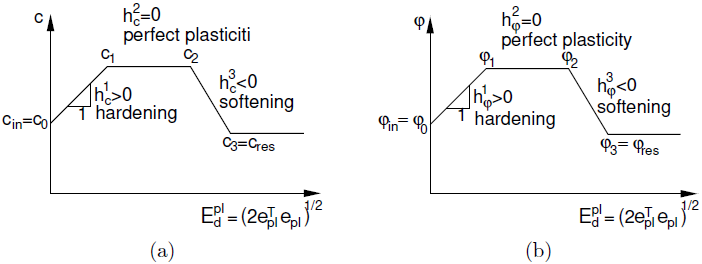 Vývoj parametrů smykové pevnosti v závislosti na ekvivalentním deviatorickém přetvoření Edpl: a) koheze c b) úhel vnitřního tření φ
Vývoj parametrů smykové pevnosti v závislosti na ekvivalentním deviatorickém přetvoření Edpl: a) koheze c b) úhel vnitřního tření φ
V případě jednoduchých laboratorních testů (např. triaxiálová komprese) za předpokladu elastické-perfektně plastické odezvy je chování modelu shodné s Drucker-Pragerovým modelem nebo Mohr-Coulombovým modelem.
Obdobné je též řešení úlohy za předpokladu odvodněných a neodvodněných podmínek. Více informací lze tedy nalézt např. v popisu Drucker-Pragerova modelu. V případě řešení úlohy za předpokladu neodvodněných podmínek a s využitím zpevnění/změkčení lze použít pouze variantu 1: Typ úlohy (1): výpočet v efektivních napětích (cef, φef).
Při modelování dilatance (vývoj kladných objemových plastických přetvoření během plastického smýkání) umožňuje Modifikovaný Mohr-Coulombův model uvažovat buď konstantní hodnotu úhlu dilatance ψ, podobně jako modely Drucker-Prager, Mohr-Coulomb, Hoek-Brown, anebo řešit vývoj úhlu dilatance výpočtem užitím modifikované Roweovy dilatanční teorie, a to následovně
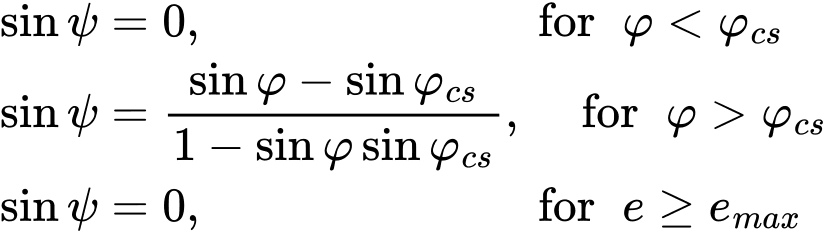
kde φ představuje aktuální hodnotu úhlu vnitřního tření a φcs je úhel vnitřního tření odpovídající kritickému stavu zeminy. Je zřejmé, že vývoj kladných objemových přetvoření lze omezit maximální hodnotou čísla pórovitosti emax podobně jako v případě Drucker-Pragerova modelu.
Materiálové parametry definující Modifikovaný Mohr-Coulombův materiálový model jsou uvedeny v následující tabulce. Parametry použité při řešení úlohy za neodvodněných podmínek, typ úlohy 2 nebo 3, lze nalézt v popisu Drucker-Pragerova modelu.
Symbol | Jednotky | Popis | |
| [MPa] | Modul pružnosti | |
| [MPa] | Modul odtížení/přitížení | |
|
| Poissonovo číslo | |
| [kPa] | Efektivní součinitel koheze | |
| [°] | Efektivní úhel vnitřního tření | |
| [°] | Úhel dilatance | |
| [kN/m3] | Objemová tíha | |
|
| Počáteční číslo pórovitosti odpovídající stavu na konci 1. fáze | |
|
| Maximální číslo pórovitosti pro ukončení dilatance (při omezení dilatance) | |
| [°] | Úhel vnitřního tření příslušný kritickému stavu (při nastavení | |
| [1/K] | Součinitel teplotní roztažnosti (při uvažování teploty) | |
| - | graf vývoje c v závislosti na |
Modifikovaný Mohr-Coulombův model umožňuje řešit také úlohu stability, a to jak standardní úlohu stability svahu, tak i úlohu stability řešenou v rámci dané fáze budování. Úloha je řešena postupnou redukcí parametrů smykové pevnosti c, φ tak, jak je vysvětleno např. v popisu Drucker-Pragerova modelu. V tomto případě je možnost modelovat zpevnění/změkčení během redukčního procesu vypnuta.
Do budoucna se předpokládá rozšíření tohoto modelu zavedením tlakového omezení podobně jako v případě Soft soil modelu.