Spencer
Die Spencer-Methode ist ein allgemeines Lamellenverfahren, das auf dem Grenzgleichgewicht beruht. Es benötigt ein befriedigendes Kräfte- und Momentengleichgewicht, das auf einzelne Blöcke wirkt. Die Blöcke (Lamellen) entstehen durch Aufteilen des Bodens über der Gleitfläche furch Trennebenen. Die Kräfte, die auf einen einzelnen Block wirken, sind in der folgenden Abbildung dargestellt:
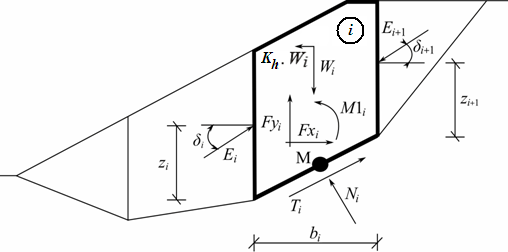Statisches Schema: Spencer-Methode
Jeder Block trägt durch diese Kräfte zum Gleichgewicht bei:
Wi | - | Blockgewicht, inklusive Materialauflast mit Gewichtscharakter (Masse) und einschließlich der Auswirkungen von Koeffizient des vertikalen Erdbebens Kv |
Kh*Wi | - | horizontale Trägheitskraft, die Erdbebeneffekte repräsentiert, Kh ist der Koeffizient der horizontalen Beschleunigung während eines Erdbebens |
Ni | - | Normalkraft auf der Gleitfläche |
Ti | - | Scherkraft auf der Gleitfläche |
Ei,Ei+1 | - | Kräfte die von benachbarten Blocks ausgeübt werden und die, von der Horizontalen aus, um den Winkel δ geneigt sind |
Fxi,Fyi | - | andere horizontale und vertikale auf den block wirkende Kräfte |
M1i | - | Moment der Kräfte Fxi, Fyi das um den Punkt M rotiert, welcher das Zentrum des i-ten Abschnitts der Gleitfläche ist |
Ui | - | Resultierende des Porenwasserdrucks auf dem i-ten Abschnitt der Gleitfläche |
Die folgenden Annahmen werden für die Spencer-Methode eingeführt, um das Grenzgleichgewicht der Kräfte und Momente der einzelnen Blöcke zu berechnen:
- Trennflächen zwischen den Lamellen sind immer vertikal
- die Wirkungslinie des Blockgewichts Wi verläuft durch die Mitte des i-ten Abschnitts der Gleitfläche, den Punkt M
- die Normalkraft Ni wirkt in der Mitte des i-ten Abschnitts der Gleitfläche, im Punkt M
- die Neigung der Kräfte Ei wirkt zwischen den Blöcken und ist konstant für alle und ist gleich δ, nur am Ende der Gleitfläche ist δ = 0
Zur Lösung werden folgende Formeln angewandt:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
wo: | φi | - | Winkel der inneren Reibung auf dem Gleitflächenabschnitt |
ci | - | Kohäsion des Bodens auf dem Gleitflächenabschnitt | |
αi | - | Neigung des Gleitflächenabschnitts |
Gleichung (1) stellt die Beziehung zwischen effektivem und Gesamtwert der Normalkraft, die auf die Gleitfläche wirkt, dar. Gleichung (2) bezieht sich auf die Bedingungen nach Mohr-Coulomb, die die Beziehung zwischen Normal- und Scherkräften auf ein gegebenen Abschnitt der Gleitfläche darstellen. Gleichung (3) stellt das Kräftegleichgewicht senkrecht zum i-ten Abschnitt dar, wohingegen Gleichung (4) das Gleichgewicht entlang dem i-ten Abschnitt der Gleitfläche darstellt. SF ist der Sicherheitsfaktor, welcher genutzt wird, um Bodenparameter abzumindern. Gleichung (5) entspricht dem Momentengleichgewicht um den Punkt M, wobei ygi die vertikale Koordinate des Angriffspunkts des Blockgewichts und yM die vertikale Koordinate des Punkts M ist.
Das Umstellen der Gleichungen (3) und (4) ergibt folgende rekursive Formel:
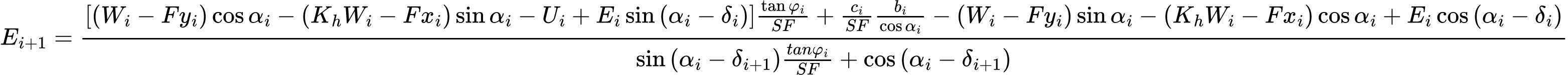
Diese Formel ermöglicht die Berechnung aller Kräfte Ei die zwischen den Blöcken wirken für gegebene Werte für δi und SF. Diese Lösung funktioniert unter der Annahme, dass der Wert E am Ursprung der Gleitfläche bekannt und gleich E1=0 ist.
Eine weitere rekursive Formel folgt aus dem Momentengleichgewicht der Gleichung (5):
Diese Formel erlaubt uns die Berechnung für gegebene Werte für δ aller Hebelarme z der Kräfte zwischen den Blöcken, bei Kenntnis des Werts am linken Rand der Gleitfläche, wo z1 = 0.
Der Sicherheitsfaktor SF wird durch Anwendung des folgenden Iterationsprozesses bestimmt:
- Der Anfangswert von δ wird gleich Null gesetzt δ = 0.
- Der Sicherheitsfaktor SF für einen Wert von δ folgt aus Gleichung (6), während man annimmt, dass En+1 = 0 am Ende der Gleitfläche ist.
- Den Wert δ liefert die Gleichung (7) indem man den Wert E, der im vorherigen Schritt ermittelt wurde mit der Anforderung dass das Moment im letzten Block gleich Null ist. Gleichung (7) liefert nicht den Wert von zn+1 da dieser gleich Null ist. Für diesen Wert muss das Momentengleichgewicht (5) erfüllt sein.
- Schritt 2 und 3 werden solange wiederholt, bis sich δ nicht mehr verändert.
Damit der Iterationsprozess stabil ist, ist es notwendig, dass instabile Lösungen vermieden werden. Solche Instabilitäten treten auf, wenn in (6) und (7) durch Null geteilt wird. In Gleichung (7) wird für δ = π/2 oder δ = -π/2 durch null dividiert. Demnach muss der Wert des Winkels δ im Intervall (-π/2 ; π/2) liegen.
Division durch Null in (6) tritt auf, wenn:
Eine weitere Kontrollmöglichkeit zur Vermeidung numerischer Instabilitäten ist die Überprüfung des Parameters mα - folgende Bedingung muss erfüllt sein:
Demnach muss man, bevor man die Iteration durchführt, den höchsten kritischen Wert von SFmin finden, der obige Bedingung erfüllt. Werte kleiner dem kritischen Wert SFmin sind im Bereich der instabilen Lösungen, demnach beginnt die Iteration bei einem Wert von SF der größer als SFmin ist und somit sind alle anderen Werte von SF ebenfalls größer SFmin.
Generell konvergieren rigorose Methoden schlechter als einfache Methoden (Bishop, Fellenius). Beispiele mit Konvergenzproblemen sind unter anderem zu steile Abschnitte der Gleitfläche, komplexe Geometrie, ein signifikanter Sprung in der Auflast, usw. Falls keine Lösung gefunden wird, empfehlen wir eine geringfügige Änderung der Eingangsdaten, z. B. eine weniger steile Gleitfläche, Eingabe von mehr Punkten für die Gleitfläche, usw. oder alternativ die Berechnung mit einfachen Methoden.
Literatur:
Spencer, E. 1967. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique, 17(1): 11-26.