Modified Mohr-Coulomb (MCM)
The Modified Mohr-Coulomb model represents a certain extension of the original Mohr-Coulomb model. The yield surface is presented, similarly to the shear yield surface of the Soft soil model, or the limit yield surface of the Hardening soil model, in the form of the Matsuoka-Nakai failure criterion. A graphical representation of the yield surface is evident from the following figure. From the projection of the yield surface into the deviatoric planes it is clear that with decreasing angle of internal friction φ the yield surface approaches the Drucker-Prager model, while for larger values of φ it approaches the Rankin yield surface. Moreover, the yield surface of the Modified Mohr-Coulomb is a smooth convex curve and passes through all vertexes of the Mohr-Coulomb model. Therefore, unlike the Drucker-Prager model, the slope of the projection into the meridian plane Mφθ is not constant but depends on the current value of the Lode angle (Mφθ = Mφθ(φ, θ)).
On the contrary, the plastic potential function, which drives the evolution of plastic strains, is identical to the one of the Drucker-Prager model. It is therefore independent of the Lode angle. Nevertheless, it depends on the dilatancy angle ψ (Mψ = Mψ(ψ)). In general we assume that φ ≠ ψ, which corresponds to the non-associated flow rule.
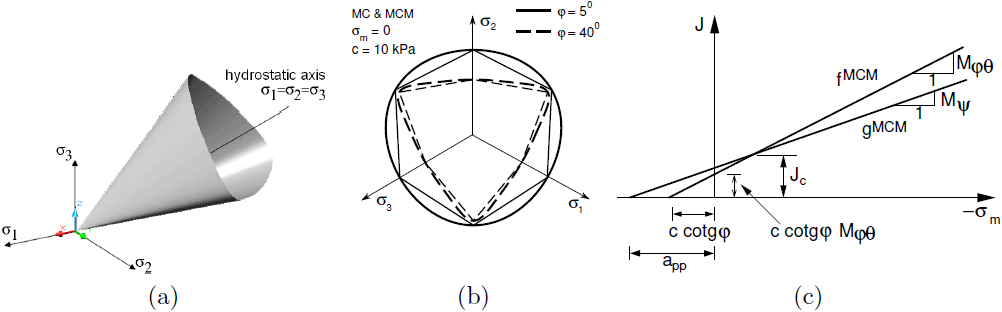 a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
a) yield surface in principal stress space, b) projection into deviatoric and c) meridian planes
Unlike all other models, regardless whether elastic-perfectly plastic or elastic-plastic with hardening/softening, the Modified Mohr-Coulomb model allows for the evolution of the yield surface as a function of the equivalent deviatoric plastic strain Edpl. More specifically, we define functions c(Edpl) and φ(Edpl). The assumed, piecewise linear, variation of strength parameters is evident from the following figure.
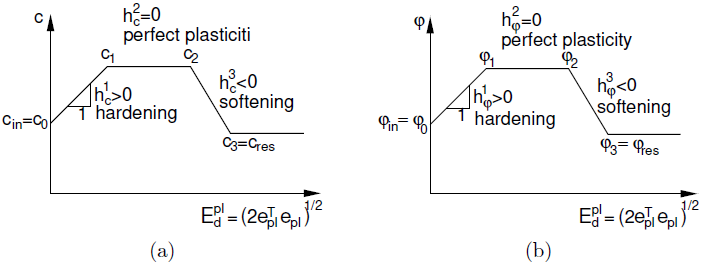 Evolution of shear strength parameters as a function of equivalent deviatoric plastic strain Edpl: a) cohesion c b) angle of internal friction φ
Evolution of shear strength parameters as a function of equivalent deviatoric plastic strain Edpl: a) cohesion c b) angle of internal friction φ
When limiting attention to simple laboratory tests (e.g., triaxial compression) and to elastic-perfectly plastic response the model provides predictions identical to that generated by the Drucker-Prager or the Mohr-Coulomb model.
The same applies to the application of drained or undrained conditions. Further information in this regard are available in the presentation of the Drucker-Prager model. When running the analysis under undrained conditions while exploiting hardening/softening features one may proceed with the Type (1): analysis in effective stress (cef, φe) only.
When modeling the effect of dilation (evolution of positive volumetric plastic strains during plastic shearing) the Modified Mohr-Coulomb model allows for considering either a constant value of the dilatancy angle ψ, similarly to the Drucker-Prager, Mohr-Coulomb, Hoek-Brown models, or to describe the evolution of ψ employing Rowe's dilation theory as follows
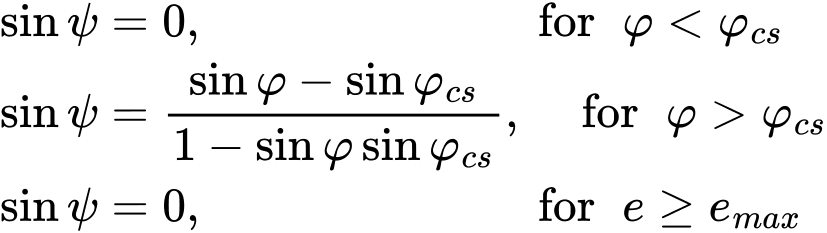
where φ represents the current value of the angle of internal friction and φcs is the critical state friction angle. Clearly, the evolution of positive volumetric strains can be limited with the help of the maximum void ratio emax as described for example for the Drucker-Prager model.
Material parameters defining the Modified Mohr-Coulomb material model are listed in the following table. Parameters used in the analysis with undrained conditions, types 2 and 3, can be found in the presentation of the Drucker-Prager model.
Symbol | Units | Description | |
| [MPa] | Modulus of elasticity | |
| [MPa] | Modulus of unloading/reloading | |
|
| Poisson's ratio | |
| [kPa] | Effective coefficient of cohesion | |
| [°] | Effective angle of internal friction | |
| [°] | Dilatancy angle | |
| [kN/m3] | Bulk weight | |
|
| Initial void ratio corresponding to the state at the end of 1st calculation stage | |
|
| Maximum void ratio to terminate dilation (when limiting dilation) | |
| [°] | Critical state friction angle (when determining | |
| [1/K] | Coefficient of thermal expansion (when considering temperature effects) | |
| - | graph describing evolution of c as a function |
The Modified Mohr-Coulomb model allows for performing the stability analysis. Both the standard slope stability analysis and stability analysis within a given construction stage can be carried out. The task is solved by gradually reducing the peak shear strength parameters c, φ in the same way as outlined for the Drucker-Prager model. During the reduction process the hardening/softening feature is turned off.
It is expected that the model will be further enhanced by introducing the cap yield surface similarly to the Soft soil model.