Cálculo de las constantes de Winkler - Pasternak desde los parámetros de deformación de suelos
Las constantes C1y C2 de Winkler - Pasternak son calculadas en el programa por las condiciones de matrices de igualdad flexibilidad de zapata continua infinitamente rígida que reposa en Winkler - Pasternak y en subsuelo elástico
El material de la capa se caracteriza por las siguientes cantidades:
Edef | - | módulo de deformación [MPa] |
ν | - | coeficiente de Poisson |
Eoed | - | módulo edométrico [MPa] |
G | - | módulo de corte [MPa] |
De estos, Edef y ν son independientes, los otros dos están determinados por relaciones:
![]()
y
![]()
La zapata corrida tiene un ancho de 2b y la zona de deformación debajo de la tira tiene un espesor de H.
Por solución de la base elástica nos referimos a encontrar la relación entre el desplazamiento y la carga de la zapata corrida en la forma:
![]()
donde P es la matriz de flexibilidad.
Resolviendo para una capa elástica isotrópica homogénea debajo de la cintura de la base evitando desplazamientos horizontales, obtenemos una matriz de flexibilidad P de la forma:
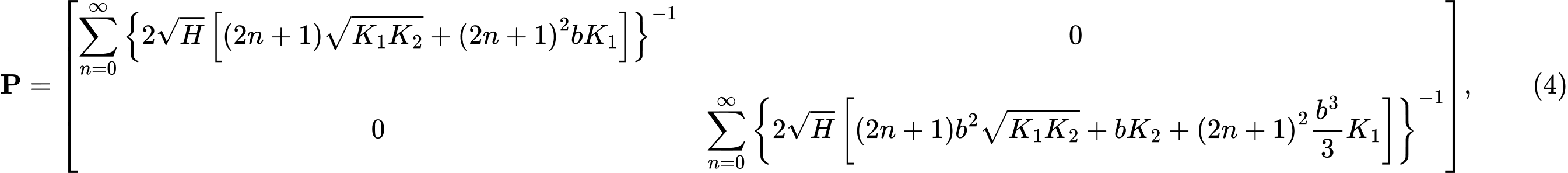
donde
![]()
y
![]()
Resolviendo la ecuación diferencial del modelo de subsuelo de dos parámetros, obtenemos una matriz P de la forma:
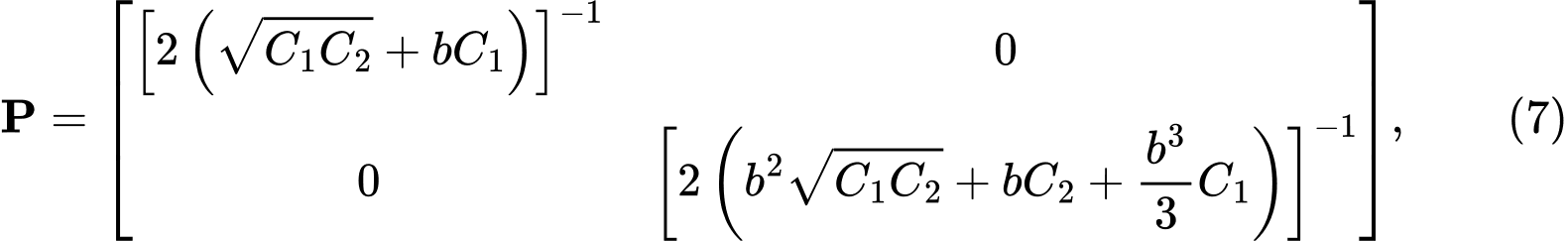
donde C1, C2 son las constantes del modelo de subsuelo de Winkler-Pasternak. Encontramos sus valores a partir de la condición de que la matriz P de la expresión (4) debe ser idéntica a la matriz P de expresión (7). Por comparación y modificación obtenemos las relaciones:
![]()
y
![]()
donde
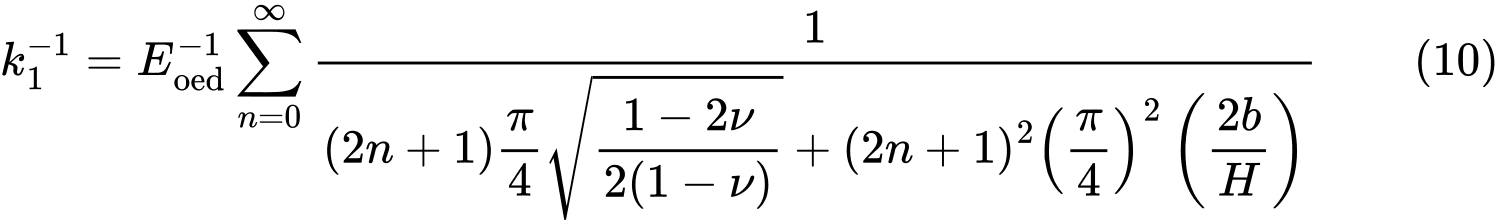
y
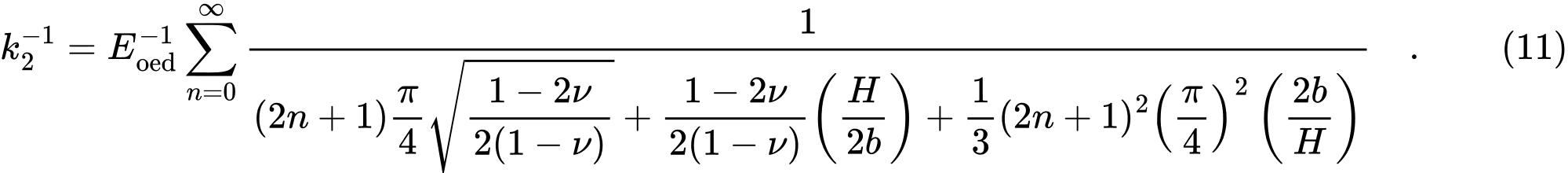
De las relaciones (8) y (9), los valores de C1 y C2, se calculan directamente, mientras que las sumas infinitas en las expresiones (10) y (11) se realizan en GEO5 para los primeros 21 sumandos.
Bibliografía:
Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984