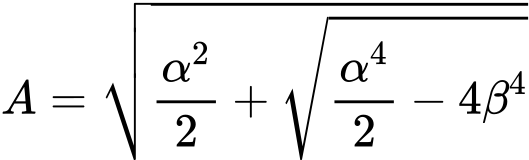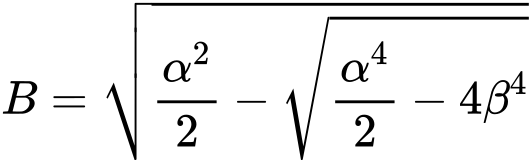Méthode géométrique (d'Euler)
Le sol entourant le micropieu est représenté dans le programme par le module de réaction du sol de fondation Ep (constante de Winkler k) défini par l'utilisateur dans le cadre "Calcul de la section". La figure ci-après illustre un modèle de structure.
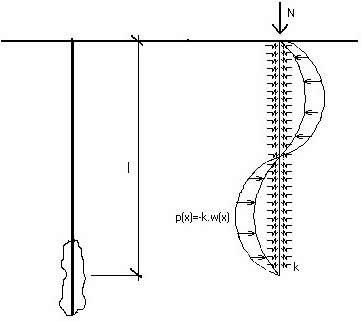Modèle de structure
Pour un micropieu en compression, on s'attend à ce qu'un nombre variable de demi-ondes se produisent en fonction de la géométrie, de la rigidité de la structure et du sol environnant. La solution dans ce cas découle de l'équation de flexion d'une poutre droite.
Après quelques manipulations, l'équation de flexion peut être exprimée comme suit :
| |
où : | |
| |
| |
| |
|
Les constantes d'intégration C1-C4 sont déterminées à partir de quatre conditions aux limites, en fonction des appuis des extrémités.
La force critique Ncr se calcule en utilisant la formule (dans [1]) :
où : | Ei | - | module d'élasticité d'une section idéale |
Ii | - | moment d'inertie d'une section idéale | |
lp | - | longueur effective du micropieu (longueur libre + 1/2 longueur du scellement) | |
Er | - | ||
n | - | nombre de demi-ondes |
La force critique Ncr est prise comme un minimum de la fonction (1). Elle est atteinte pour la longueur de la demi-onde :
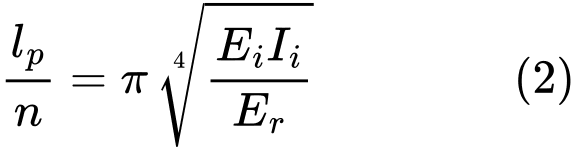
Le nombre de demi-ondes n découle de la relation (2) :
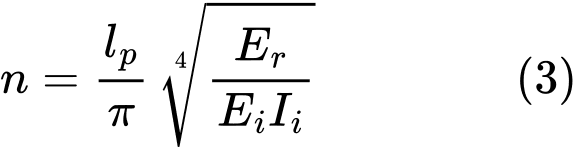
Si une partie du micropieu dépasse au dessus du terrain (décalage de la tête du pieu), les valeurs réduites de n et Er se calcule comme suit :
où : | lv | - | longueur du micropieu au dessus du terrain |
En supposant une condition de charnière-charnière, l'équation suivante est utilisée :
En supposant une condition de charnière-fixe, l'équation suivante est utilisée :
Littérature:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936