Ajuda Online

Tassement primaire

Le tassement primaire final s est souvent remplacé par le terme tassement. La plupart des procédures de calcul peuvent être classées en deux groupes :

• Déformation élastique linéaire
• Déformation élastique non linéaire

Déformation élastique linéaire

La relation contrainte-déformation linéaire suit la loi de Hooke :

L'utilisation du module de Young E (souvent appelé module d'élasticité) n'est valable que si la charge est autorisée à s'étirer dans le sens horizontal, ce qui ne s'applique en fait qu'aux fondations de petite taille. Si la charge s'applique sur une zone plus grande, le sol contraint ne peut se déformer latéralement, à l'exception de ses bords, et ne subit donc qu'une contrainte verticale (unidimensionnelle) liée au module œdométrique E_oed, supérieur au module d'élasticité E.

Le tassement d'une couche de sol s est déterminé en multipliant la déformation de la couche de sol ε par l'épaisseur de la couche (hauteur) H_o :

En cas de sous-sol en couches, le tassement total s'obtient en additionnant les tassements de chaque couche :

Déformation élastique non linéaire

Pour la plupart des sols, la relation contrainte-déformation est non linéaire et est souvent influencée par l’historique de charge. Cette non-linéarité ne peut être négligée, en particulier lors du calcul du tassement des sols à grains fins (limons, argiles). Clairement, la procédure basée sur le module d'élasticité de Young n'est pas généralement applicable. Même en utilisant le module de déformation œdométrique dépendant des contraintes, il ne sera pas possible de produire des estimations raisonnables du comportement de certains sols surconsolidés. La déformation élastique non linéaire est généralement modélisée en utilisant l'indice des vides et les caractéristiques de déformation dérivées de la déformation unidimensionnelle d'un échantillon de sol (par exemple, constante de compression, indice de compression, etc.).

La procédure de calcul du tassement d'une couche de sol saturée compressible à l'aide de l'indice des vides e est décrite pour l'élément de sol ayant une hauteur H_o et une largeur B de 1 m :

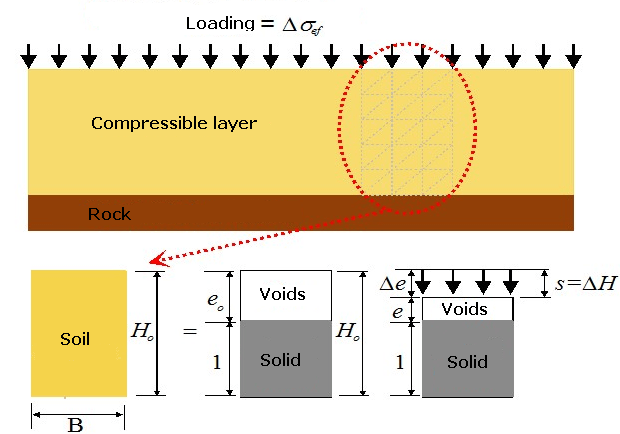Calcul du tassement à partir du diagramme de phase

Du fait que le sol est un milieu triphasique (il contient des particules solides et des pores remplis de fluide et de gaz), il est possible de décrire les particules solides (particules de roche et grains minéraux) par leur volume V_s (supposé unitaire), alors que la phase poreuse peut être décrite à l'aide de l'indice des vides e.

L'élément de sol est soumis sur sa surface supérieure à une charge uniforme q provoquant la variation de la contrainte à l'intérieur de l'échantillon ainsi que le déplacement vertical ΔH, ce qui entraîne ensuite la réduction des pores V_p et donc la réduction de l'indice des vides (de sa valeur initiale e_o à une nouvelle valeur e). La déformation verticale ε de l'échantillon de sol est donnée par le rapport de ΔH sur la hauteur d'origine de l'échantillon H_o et peut être exprimée à l'aide de l'indice des vides e selon :

En modifiant cette équation, la formule décrivant le tassement de l’échantillon à l’aide de l'indice des vides est donnée par la relation :