Oedometric Modulus
If the results from oedometric test are represented in terms of oedometric curve (Δε = f(Δσef )), it becomes evident that for each point on the curve we receive a different ratio σef /ε.
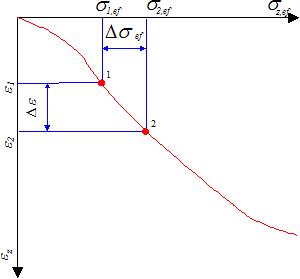 Determination of oedometric modulus Eoed
Determination of oedometric modulus Eoed
If the stress-strain curve is replaced for a certain interval of two neighboring stresses σ1ef - σ2ef by a secant line, it is acceptable to assume a linear behavior of soil within this interval and represent the soil compressibility by as Δσef/Δε - called the oedometric modulus of deformation. The oedometric modulus of deformation is, therefore, a secant modulus linked to a certain stress interval σ1ef - σ2ef selected on the stress-strain diagram Δε = (Δσef ):
![]()
In general, the oedometric modulus of deformation Eoed tends to decrease its value with the increasing stress interval. Therefore we should consider for each layer a specific value of Eoed pertinent to a given stress interval (from original to final stress state). This is reflected in the program by the way of inputting Eoed, where it is possible to specify for each soil the respective oedometric curve (σef/ε diagram).
Practical experience, however, suggests (e.g. for clays) several orders of magnitude difference between the value of Eoed derived from the deformation modulus Edef and that provided by the in situ measured loading curve.
The relation between Edef and Eoed is provided by:
![]()
![]()
where: | ν | - | Poisson's ratio |
Edef | - | deformation modulus |
Approximate range of values of oedometric modulus of deformation Eoed for individual soils and typical stress range (prof. I. Vanicek: Soil mechanics):
Soil | Oedometric modulus Eoed [MPa] |
gravels | 60 - 600 |
medium dense sands to dense sands | 7 - 130 |
cohesive | 2 - 30 |
Literature:
Vanicek, I.: Geomechanika 10: mechanika zemin. 3th edition, Prague, CTU, 2000, 229 s., ISBN 80-01-01437-1.