Ajuda Online

Osiadanie pierwotne

Końcowe osiadanie pierwotne jest często zastępowane terminem osiadania. Większość podejść obliczeniowych można przypisać do jednej z dwóch grup:

• Liniowa deformacja sprężysta
• Nie liniowa deformacja sprężysta

Liniowa deformacja sprężysta

Liniowa zależność naprężenie - odkształcenie wynika z prawa Hook’a:

Zastosowanie modułu sprężystości E Young'a jest zastępowane tylko w przypadkach, gdzie dopuszcza się rozszerzenie gruntu w kierunku poziomym. Jednak, jest to do przyjęcia tylko dla małych fundamentów bezpośrednich. Przy stosowaniu obciążenia na większej powierzchni, naprężony grunt nie może - za wyjątkiem krawędzi - odkształcać się na boki i doświadcza zatem tylko odkształcenia pionowego (jednowymiarowego) związanego z modułem edometrycznym E_oed, który jest większy od modułu sprężystości E.

Osiadanie warstwy gruntu s jest wyznaczane poprzez pomnożenie deformacji warstwy gruntu ε przez miąższość warstwy (wysokość) H_o:

W przypadku podłoża uwarstwionego otrzymujemy całkowite osiadanie przez dodanie osiadań poszczególnych warstw:

Nieliniowa deformacja sprężysta

Dla większości gruntów, zależność naprężenie - odkształcenie jest nieliniowe i często wpływa na nią historia obciążeń. Nie można pomijać tej nieliniowości zwłaszcza przy obliczaniu osiadania gruntów drobnoziarnistych (iły, gliny). Oczywiście, procedura oparta na zastosowaniu modułu sprężystości Young'a nie jest ogólnie stosowana. Nawet przy zastosowaniu modułu edometrycznego deformacji zależnego od naprężenia, nie można uzyskać rozsądnych danych szacunkowych zachowania pewnych gruntów prekonsolidowanych. Nieliniowa deformacja sprężysta jest modelowana za pomocą wskażnika porowatości i właściwości deformacji uzyskanych z jednowymiarowego odkształcenia próbki gruntu (np. stała ściskania, wskaźnik ściśliwości, itp.).

Procedura obliczania osiadania nawodnionej warstwy gruntu za pomocą porowatości e została opisana na następującym elemencie gruntu posiadającym wysokość H_o i szerokość B = 1m:

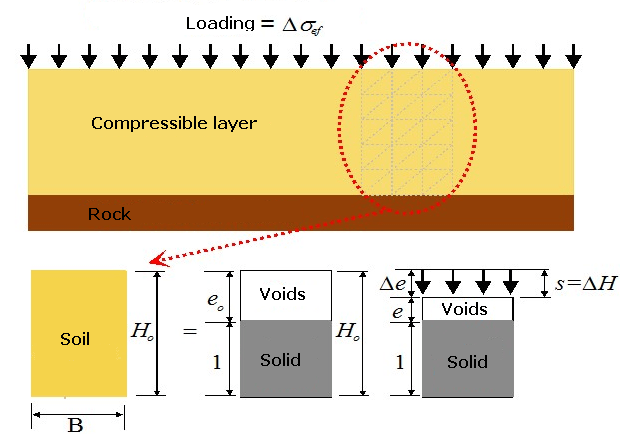Analiza osiadania z wykresu fazowego

Ze względu na fakt, że grunt jest medium trójfazowym (zawiera cząstki stale i pory wypełnione cieczą i gazem), istnieje zatem możliwość opisania cząstek stałych (cząstki skał i ziarna mineralne) poprzez ich objętość V_s (równa jedności), natomiast fazę porowatą można opisać współczynnikiem porowatości e.

Element gruntu poddawany jest w swej górnej powierzchni jednolitemu obciążeniu q powodującemu zamianę naprężenia wewnątrz próbki, a także przesunięcie pionowe ΔH, które z kolei prowadzi do redukcji porów V_p, a zatem także do redukcji współczynnika porowatości (od swej wartości początkowej e_o do nowej wartości e). Odkształcenie pionowe ε próbki gruntu dane jest ze stosunku ΔH do początkowej wysokości próbki H_o, i można je wyrazić za pomocą wskaźnika porowatości e:

Poprzez zmodyfikowanie tego równania otrzymujemy wzór opisujący osiadanie próbki za pomocą współczynnika porowatości: