Symetria osiowa
Ten model obliczeniowy jest odpowiedni do obliczeń konstrukcji osiowo symetrycznych (obrotowych). Założenie to musi być spełnione zarówno w odniesieniu do konstrukcji jak i obciążeń. Typowe przykłady takich zadań to: analiza pojedynczego pala obciążonego siłą pionową, głęboki wykop o kształcie kołowym czy pompowanie wody z okrągłego otworu.
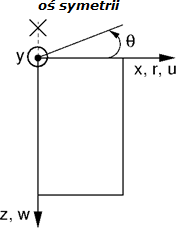 Analiza zagadnień osiowo symetrycznych
Analiza zagadnień osiowo symetrycznych
Podobnie jak w zagadnieniach modelowanych w płaskim stanie odkształcenia i w tym przypadku zagadnienie obliczeniowe jest trójwymiarowe, może być jednak sprowadzone do zagadnienia dwuwymiarowego (patrz Rysunek). Obliczenia są wówczas prowadzone w odniesieniu do 1 m długości łuku o średnicy równej x(r). Oś symetrii zawsze odpowiada początkowi współrzędnej x(r). Składowe naprężeń ścinających w kierunku obrotu mogą być pominięte. Pozostają zatem składowe wektorów odkształcenia i naprężenia oddziałujące na płaszczyznę przekroju symetrycznego oraz składowe wektorów odkształcenia i naprężenia w kierunku obwodowym. Odpowiednie niezerowe składowe wektorów naprężenia i odkształcenia są następujące:
![]()
![]()
Oczywistym jest, że odkształcenie obwodowe, a przez to także wymuszone naprężenie normalne, przyjmują wartość nieskończoną w osi symetrii. Dlatego też, uwzględniając aproksymację elementów skończonych, uzyskanie wiarygodnych wyników o właściwej dokładności wymaga zastosowania stosunkowo gęstej siatki wzdłuż osi symetrii.
Przyłożenie obciążeń liniowych i powierzchniowych jest także warte omówienia. Kilka przykładów przyłożenia obciążeń na powierzchni terenu pokazano na kolejnym Rysunku. Ewidentne jest, że ich wpływ zwiększa się wraz z odległością od osi symetrii. W związku z tym zdefiniowanie tego typu obciążenia w osi symetrii nie daje żadnego efektu. W takim przypadku konieczne jest dokonanie rodzaju obciążenia osi symetrii. Program umożliwia zdefiniowanie wyłącznie sił skupionych.
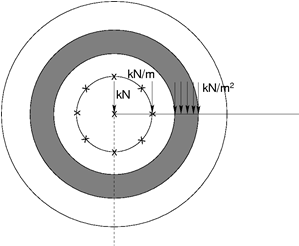 Przykłady obciążeń przyłożonych na powierzchni terenu
Przykłady obciążeń przyłożonych na powierzchni terenu
W przypadku elementów belkowych rozwiązanie odpowiada rozwiązaniu płaskiej membrany osiowo symetrycznej z uwzględnieniem efektów zginania. Niezerowe stopnie swobody są przyjęte analogicznie dla elementów belkowych w analizie w płaskim stanie odkształcenia. Oprócz efektów osiowych (południkowych) należy również uwzględnić efekty membrany oraz zginania w kierunku obwodowym (patrz kolejny Rysunek).
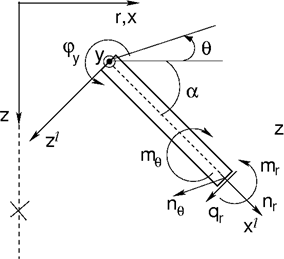 Element belkowy w symetrii osiowej
Element belkowy w symetrii osiowej
Odpowiednie składowe sił wewnętrznych (patrz Rysunek) w odniesieniu do 1 m szerokości przekroju wyznacza się następująco:
![]()
W specyficznym przypadku płyty kołowej (kąt α = 0) można odnieść się do promieniowych i obwodowych składowych sił wewnętrznych (patrz kolejny Rysunek).
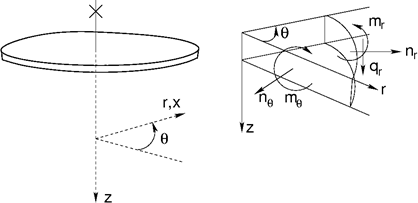 Siły wewnętrzne w płycie kołowej
Siły wewnętrzne w płycie kołowej
Siły wewnętrzne są związane z odpowiednimi odkształceniami i krzywiznami w sposób następujący:
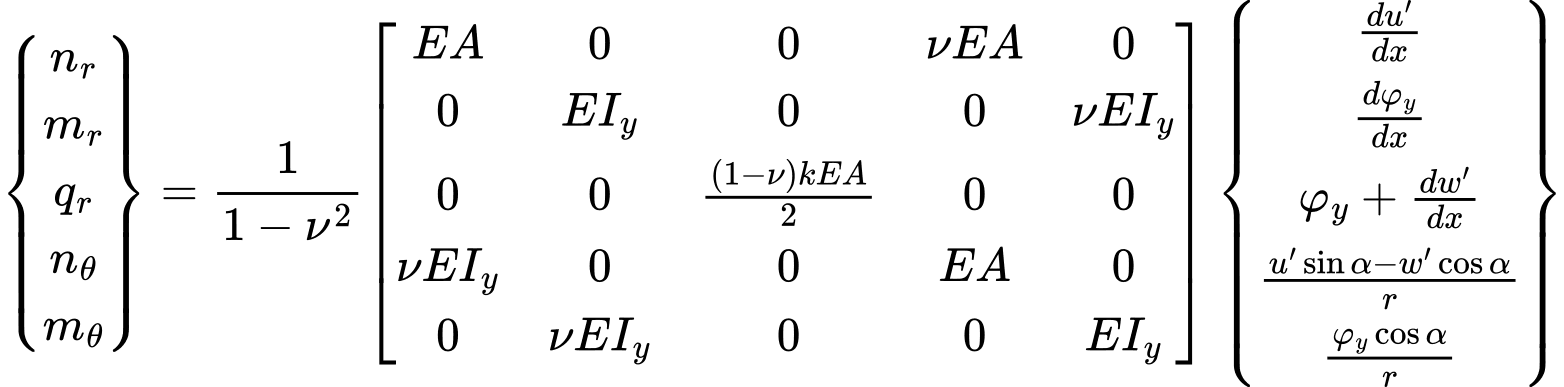
Przyjmując r dążące do nieskończoności uzyskuje się warunki płaskiego stanu odkształcenia. Należy także zauważyć, że wartości sił tnących (w przeciwieństwie do analizy w płaskim stanie odkształcenia) są silnie zależne od zagęszczenia siatki elementów skończonych. Podobnie jest w przypadku reakcji pionowych.
Uwaga do przepływu wody
Podobnie jak w przypadku sił reakcji w obliczeniach naprężeń przepływy punktowe o zdefiniowanej wartości ciśnień porowych są analizowane w odniesieniu do 1 m długości łuku o średnicy równej x(r). W analizie zagadnień w płaskim stanie odkształcenia odpowiednie wartości brane są na 1 m bieżący. Odpowiednie przepływy całkowite (napływ/wypływ) mogą być wyznaczone na podstawie przepływów punktowych [m3/dobę/m] w następujący sposób:
Analiza w płaskim stanie odkształcenia
![]()
Analiza zagadnienia osiowo symetrycznego
![]()
gdzie N oznacza liczbę węzłów wzdłuż danej linii siatki, w których obliczane są przepływy punktowe Qi [m3/dobę/m]. W przypadku analizy zagadnienia symetrii osiowej xi reperezentuje współrzędną x-ową danego punktu. Z tego względu, w symetrii osiowej otrzymuje się całkowity napływ/wypływ [m3/dobę] przez np. powierzchnię cylindryczną (linia pionwa) lub powierzchnię kołową (linia pozioma).