Wyliczenie stałych Winklera-Pasternaka z parametrów odkształceniowych gruntów
Stałe Winklera - Pasternaka C1 i C2 obliczane są w programie z warunku jednakowych macierzy sztywności nieskończenie sztywnej nieskończonej ławy fundamentowej spoczywającej na podłożu Winklera-Pasternaka i podłożu sprężystym.
Materiał warstwy charakteryzują następujące parametry:
Edef | - | moduł odkształcenia [MPa] |
ν | - | współczynnik Poissona |
Eoed | - | moduł edometryczny [MPa] |
G | - | moduł sprężystości na ścinanie [MPa] |
Z powyższych, Edef oraz ν są niezależne, pozostałe dwa parametry wyznaczane są ze wzorów:
![]()
oraz
![]()
Ława fundamentowa ma szerokość 2b i strefa deformacji pod ławą ma wysokość H.
Przez rozwiązanie podłoża sprężystego rozumiemy znalezienie zależności pomiędzy przemieszczeniem a obciążeniem stopy fundamentowej w postaci:
![]()
gdzie P jest macierzą sztywności.
Rozwiązując izotropową jednorodną warstwę sprężystą pod ławą fundamentową, unikając przemieszczeń poziomych, otrzymujemy macierz sztywności P w postaci:
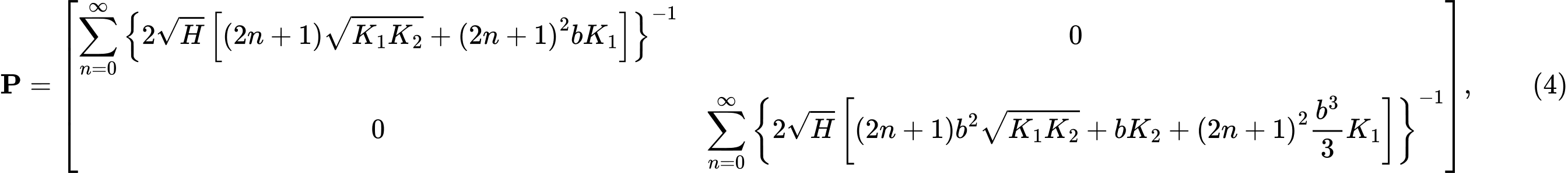
gdzie
![]()
oraz
![]()
Rozwiązując równanie różniczkowe dla dwuparametrowego modelu podłoża, otrzymujemy macierz P w postaci:
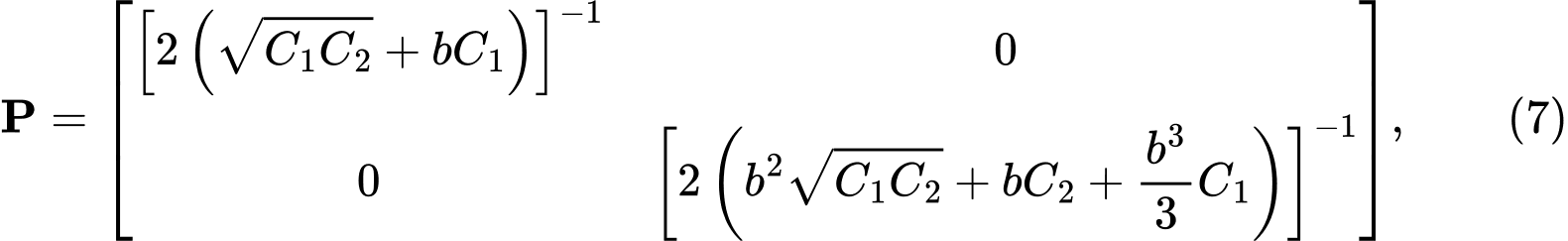
gdzie C1, C2 są stałymi modelu podłoża Winklera-Pasternaka. Ich wartości określamy z warunku, że macierz P we wzorze (4) musi być identyczna jak macierz P we wzorze (7). Przez porównanie i modyfikację uzyskujemy następujące zależności:
![]()
oraz
![]()
gdzie
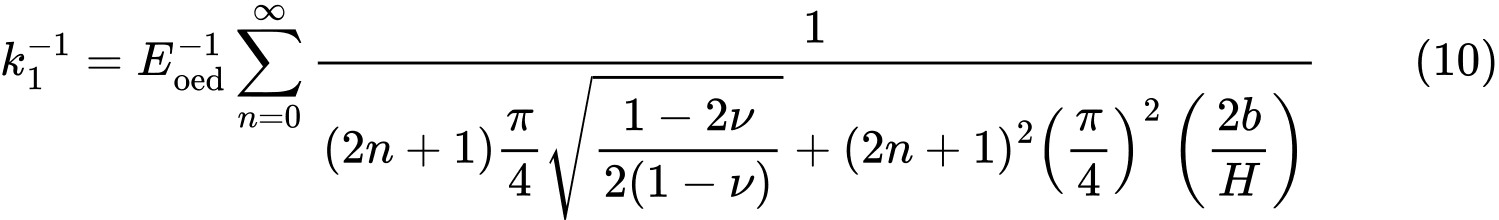
oraz
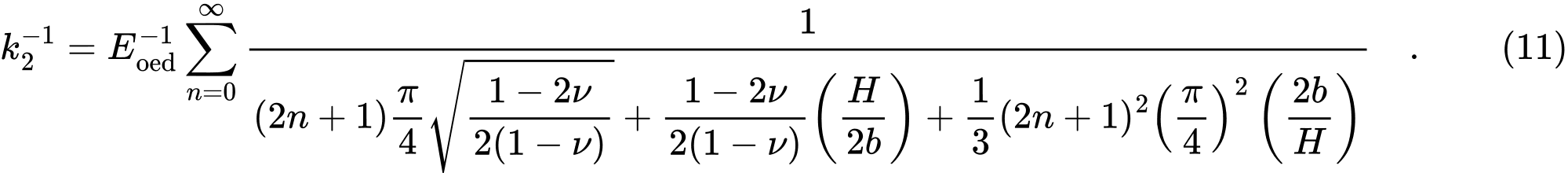
Z zależności (8) i (9), wartości C1 i C2, są bezpośrednio wyznaczane, podczas gdy nieskończone sumy w wyrażeniach (10) i (11) są wykonywane w GEO5 dla pierwszych 21 sum.
Literatura: Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984