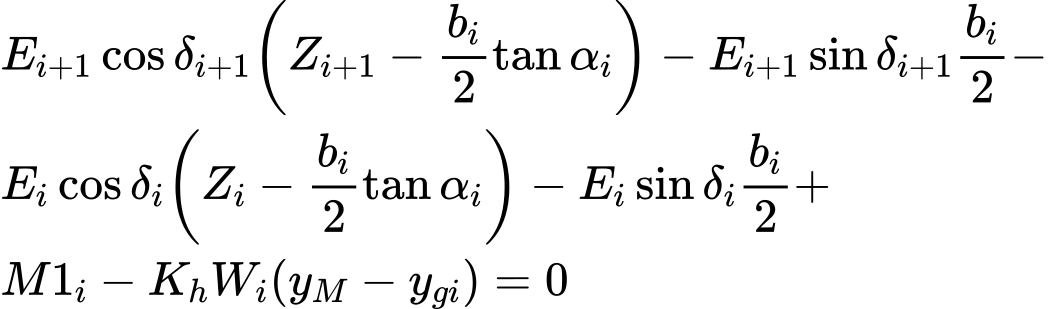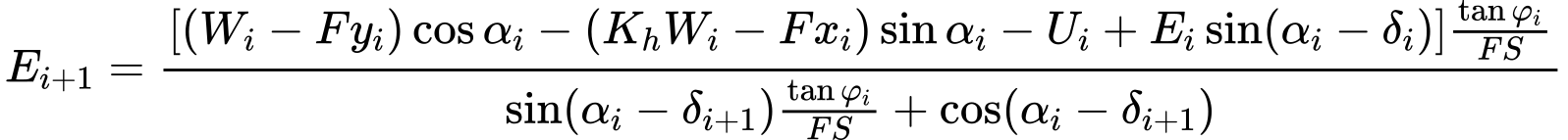Моргенштерн-Прайс
Метод Моргенштерн-Прайса является общим методом отсеков, разработанным на основе предельного равновесия. Он требует удовлетворения равновесия сил и моментов, действующих на отдельные блоки. Блоки создаются путем разделения участка грунта над поверхностью скольжения плоскостями. Статическая схема блоков и сил действующих на блоки, представлена на следующем рисунке:
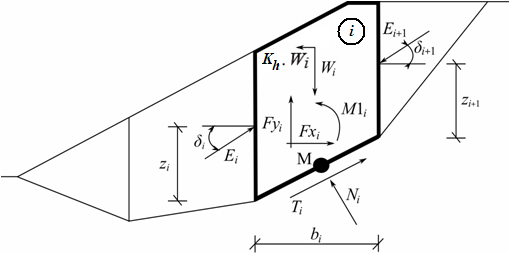Статистическая схема: метод Моргенштерн-Прайса
Предполагается, что каждый блок испытывает те же усиления, что и в методе Спенсера. Для расчета предельного равновесия сил и моментов на отдельных блоках по методу Моргенштерн-Прайса используются следующие допущения:
- | плоскости раздела между блоками всегда вертикальны |
- | линия действия веса блока Wi проходит через центр i-ого сегмента поверхности скольжения, представленного точкой M |
- | нормальная сила Ni действует в центре i-ого сегмента поверхности скольжения, в точке М |
- | наклонение сил Ei, действующих между блоками, различно на каждом блоке (δi), на крайних точках поверхности скольжения δ = 0 |
Единственное различие между методами Спенсера и Моргенштерн-Прайса состоит в указанных выше предположениях. Выбор углов наклона δi сил Ei, действующих между блоками, представлен с помощью функции полу-синуса: на рисунке показана одна из выбранных автоматически функций. Выбор формы функции оказывает незначительное влияние на конечные результаты, но правильно сделанный выбор может повысить конвергентность метода. Функциональное значение функции полу-синуса f(xi) на граничной точке xi, умноженное на величину λ, дает значение угла наклонения δi.
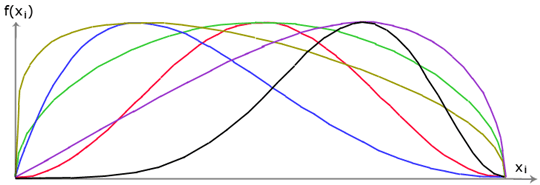Функция полу-синуса
Решение принимает следующие выражения (как метод Спенсера):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
где: | φi | - | угол внутреннего трения грунта на сегменте поверхности скольжения |
ci | - | удельное сцепление грунта на сегменте поверхности скольжения | |
αi | - | уклон сегмента поверхности скольжения |
(1) отношение между эффективным и общим значением нормальной силы, действующей на поверхность скольжения
(2) условие Мора-Кулона, представляющее отношение между нормальной и сдвиговой силами на данном сегменте поверхности скольжения (Ni и Ti)
(3) уравнение равновесия силы в направлении под прямым углом к i-ому сегменту поверхности скольжению
(4) уравнение силы равновесия вдоль i-ого сегмента поверхности скольжения
(5) уравнение момента равновесия вокруг точки M
Изменяя уравнения (3) и (4), получаем следующую рекурсивную формулу (6):
| (6) |
Эта формула позволяет рассчитать все силы Ei, действующие между блоками для данных значений δ и FS. Это решение допускает, что в начале поверхности скольжения значение E известно и равно E1=0.
Дополнительная формула для расчета угла δi (7) выводится из уравнения момента равновесия (5):
| (7) |
Эта формула позволяет рассчитать для данных значений δi все плечи zi сил, действующих между блоками, зная значение слева в начале поверхности скольжения, где z1=0.
Коэффициент надежности FS определяется при помощи следующего итерационного процесса:
1. | Начальное значение δi устанавливается в соответствии с функцией полу-синуса (δi = λ*f(xi)). |
2. | Коэффициент надежности SF для данного значения δi следует из уравнения (6), при этом допускается значение En+1 = 0 в конце поверхности скольжения. |
3. | Значение δi рассчитывается уравнением (7) с помощью значений Ei, определенных на предыдущем этапе при условии, что момент на последнем блоке равен 0. Функциональные значения f(xi) остаются неизменными на протяжении всей итерации, вычисляется лишь величина λ. Уравнение (7) не определяет значение zn+1, поскольку оно равно 0. Для этого значения должно выполняться уравнение момента равновесия (5). |
4. | Этапы 2 и 3 повторяются до тех пор, пока значение δi (соответственно величина λ) не измениться. |
Для обеспечения устойчивости процесса итерации необходимо избегать неустойчивых условий. Такие нестабильности появляются в точках, где имеет место деление на 0 в выражениях (6) и (7). В уравнении (7) деление на 0 принимается для δ = π/2 или δ = -π/2. Таким образом, значение угла δi должно находиться в интервале (-π/2;π/2).
Деление на 0 в выражении (6) имеет место, когда:
Еще одним способом предупредить числовую нестабильность является проверка параметра mα: должно выполняться следующее условие:
Таким образом, перед началом итерации необходимо найти наивысшие показатели критических значений (SFmin), удовлетворяющих выше указанные условия. Значения ниже данного критического значения SFmin находятся в области неустойчивого решения, таким образом, итерация начинается с установки SF на значение «слегка» выше SFmin, и все получаемые значения SF из итерации выше, чем SFmin.
В общем можно сказать, что сложные методы труднее подвергаются конвергенции чем более простые методы (Bishop, Fellenius). Проблемы с конвергенцией возникают напр., на участках поверхности скольжения повышенной крутизны, сложной геометрии, при резком увеличении пригрузки и т.п. В случае, что расчёт не даёт результата, рекомендуется немного изменить задание, напр., уменьшить крутизну, в поверхность скольжения добавить больше точек и т.п. или выполнить расчёт по более простому методу.
Литература:
Morgenstern, N.R., and Price, V.E. 1965. The analysis of the stability of general slip surfaces. Géotechnique, 15(1): 79-93.
Morgenstern, N.R., and Price, V.E. 1967. A numerical method for solving the equations of stability of general slip surfaces. Computer Journal, 9: 388-393.
Zhu, D.Y., Lee, C.F., Qian, Q.H., and Chen, G.R. 2005. A concise algorithm for computing the factor of safety using the Morgenstern-Price method. Canadian Geotechnical Journal, 42(1): 272-278.