Шахунянц
Метод Шахунянца - это общий метод отсеков предельного равновесия, основанный на удовлетворении условия равновесия сил на отдельных блоках. Блоки образуются в результате разбивки области над поверхностью скольжения плоскостями сечения. Статическая схема блоков и сил, действующих на них отображена на рисунке:
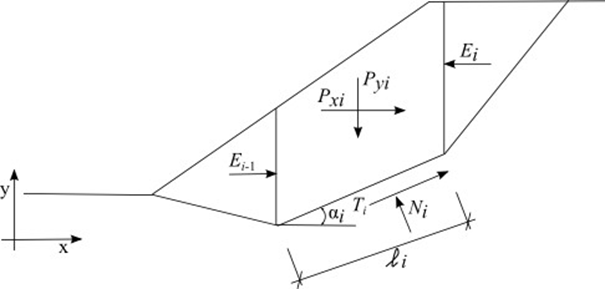 Статическая схема - Метод Шахунянца
Статическая схема - Метод Шахунянца
На каждом блоке предполагается воздействие следующих сил:
где: | Pyi | - | вертикальная равнодействующая сил на блоке ( вес блока, пригрузка блока, сейсмика, усилие анкеров, …) |
Pxi | - | горизонтальная равнодействующая сил на блоке (пригрузка блока, сейсмика, усилие анкеров, армировка грунта) | |
Ei+1, Ei | - | силы между блоками | |
Ni | - | реакция под блоком в перпендикулярном направлении к отсеку поверхности скольжения | |
Ti | - | сила трения на отсеке поверхности скольжения | |
αi | - | угол наклона отсека поверхности скольжения | |
li | - | длина отсека поверхности скольжения | |
φi | - | угол внутреннего трения грунта на отсеке поверхности скольжения | |
ci | - | удельное сцепление грунта на отсеке поверхности скольжения |
Для расчёта предельного равновесия сил на блоках метод Шахунянца вводит следующие предпосылки:
- поверхности разделяющие блоки всегда вертикальны
- наклон межблочных сил Ei равен нулю, силы действуют в горизонтальном направлении
Порядок решения:
Силы Pyi и Pxi при помощи отношений (1), (2) трансформируются в направления сил Ti и Ni. При этом для угла αi со знаком +(одинаково на схеме) сила PNi направлена против силы Ni, и сила PQi направлена против силы Ti.
![]() (1)
(1)
![]() (2)
(2)
На отсеке поверхности скольжения между силами действует отношение:
![]() (3)
(3)
где: | Ui | - | поровое давление на отсеке поверхности скольжения |
На блоке действуют условия сложения равновесия:
Условие в перпендикулярном направлении к отсеку поверхности скольжения:
![]() (4)
(4)
Условие в горизонтальном направлении к отсеку поверхности скольжения:
![]() (5)
(5)
Подставляя отношение (3) в уравнение (5), получаем уравнение:
![]() (6)
(6)
Далее, подстановкой отношения (4) в уравнение (6) получаем уравнение:
![]() (7)
(7)
После преобразований:
![]() (8)
(8)
Применением математического отношения:
![]() (9)
(9)
уравнение (8) принимает вид:
![]() (10)
(10)
Из последующих преобразований:
![]() (11)
(11)
вытекает рекуррентное отношение для межблочных сил Ei:
![]() (12)
(12)
На этом этапе в расчёт вводится коэффициент устойчивости склона Ku. Коэффициент устойчивости - это значение, с помощью которого силы, действующие на отдельные блоки грунта приведены в состояние предельного равновесия. Предельное равновесие достигается тем, что на коэффициент устойчивости перемножаются активные силы, т.е. силы, воздействие которых способствует движению массива над поверхностью скольжения по направлению вниз. Активные силы в выражении (12) отражены в члене PQi. В нём находятся и активные силы, которые способствуют сползанию блока, но также и силы, удерживающие блок от сползания. Активные силы, способствующие сползанию имеют условное обозначение PQi,sd, силы, удерживающие сползание блока получают обозначение PQi,ud. Следовательно отношение (12) приобретает вид:
![]() (13)
(13)
При значении PQi со знаком +, сила способствует оползанию склона и будет рассмотрена как активная сила PQi,sd. При значении PQi со знаком -, сила удерживает сползание склона и будет рассмотрена как PQi,ud. Следовательно, вычитание значения PQi,ud, со знаком - в выражении (13) - это фактическое прибавление плюсового значения, следовательно, можно формально записать:
![]() (14)
(14)
В начале поверхности скольжения значение равно E0 = 0. Следовательно, для значения E1 действует:
![]() (15)
(15)
Значение E2, следовательно, представлено:
![]() (16)
(16)
Подобным образом можно определить значения всех остальных межблочных сил, причём соблюдается правило, что на последнем блоке в конце поверхности скольжения должно равняться En = 0. В соответствии с предыдущими отношениями это можно записать:
![]() (17)
(17)
Из данного уравнения прямо вытекает выражение для расчёта коэффициента устойчивости Ku:
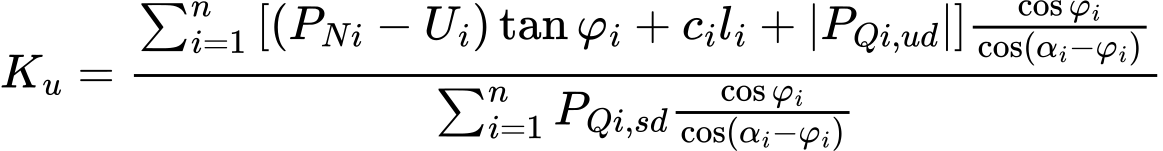 (18)
(18)