Line Surcharge - Active Earth Pressure
Vertical infinitely long line load f acting on the ground surface parallel with structure leads to a triangular increment of active earth pressure applied to the structure over a given segment hf - see figure:
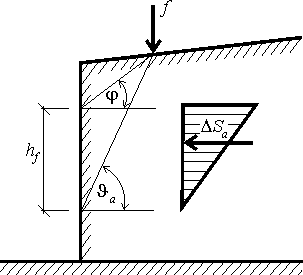 Diagram of increment of active earth pressure due to vertical line load acting on ground surface
Diagram of increment of active earth pressure due to vertical line load acting on ground surface
Action of the line surcharge is determined such that two lines are drawn from the point of application following angles φ and ϑa (corresponding to the critical slip surface), which is provided by:
![]()
where: | φ | - | angle of internal friction of soil |
ε | - | angle derived from the following formulas |
![]()
![]()
![]()
where: | β | - | slope inclination |
φ | - | angle of internal friction of soil | |
δ | - | angle of friction between structure and soil | |
α | - | back face inclination of the structure | |
c | - | cohesion of soil | |
γ | - | unit weight of soil | |
h | - | assumed depth |
For non-homogeneous soil and inclination of ground surface β smaller than the angle of internal friction of the soil φ the value of the angle ε is given by:
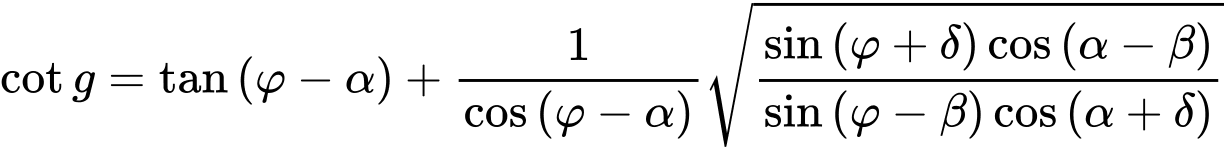
where: | β | - | slope inclination |
φ | - | angle of internal friction of soil | |
δ | - | angle of friction between structure and soil | |
α | - | back face inclination of the structure |
The resultant of the increment of active earth pressure due to line load f is provided by:
![]()
where: | ϑa | - | angle of the critical slip plane |
φ | - | angle of internal friction of soil | |
δ | - | angle of friction between structure and soil | |
f | - | magnitude of line surcharge |
For non-homogeneous soils the program proceeds as follows.