Hoek-Brown
O modelo material de Hoek-Brown é a condição de cedência mais comum para descrever o comportamento não linear de maciços rochosos. De forma semelhante ao modelo material de Mohr-Coulomb, o modelo de Hoek-Brown é formulado com base em três funções de cedência com projeção no plano de desvio com a forma de hexágono irregular. No entanto, ao contrário ao modelo de Mohr-Coulomb, a projeção da superfície de cedência fHB no plano meridiano é descrita por uma função não linear. Tal como no modelo de Mohr-Coulomb, o critério de cedência de Hoek-Brown é uma função da tensão efetiva média σmeff e do ângulo de Lode θ.
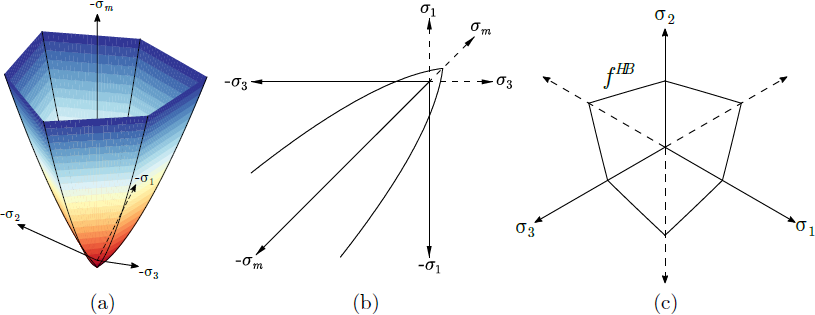a) superfície de cedência no espaço de tensão principal, b) projeção no plano de tensão máxima e principal e c) projeção no plano de desvio
O modelo de Hoek-Brown é puramente empírico e a sua formulação baseia-se no Geological strength index GSI (o valor de GSI = 100 corresponde a uma rocha intacta e tende para zero em função do deterioramento da qualidade da rocha), o fator de distúrbio D (considera atividades no subsolo como mineração e escavação; o valor D = 0 corresponde a uma rocha intacta e o valor D = 1 corresponde ao nível máximo de danos/alteração na rocha), a resistência à compressão da rocha intacta σci e o parâmetro mi. Os últimos dois parâmetros são determinados a partir do ensaio triaxial. O valor máximo fisicamente aceitável para a resistência à tração 
é dado por
onde o parâmetro s e a constante de Hoek-Brown reduzida mb são exprimidos como parâmetros GSI e D como
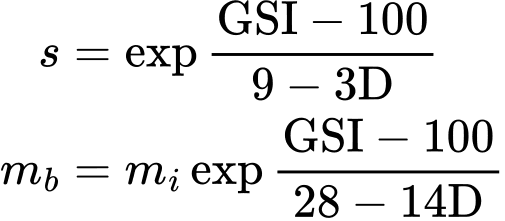
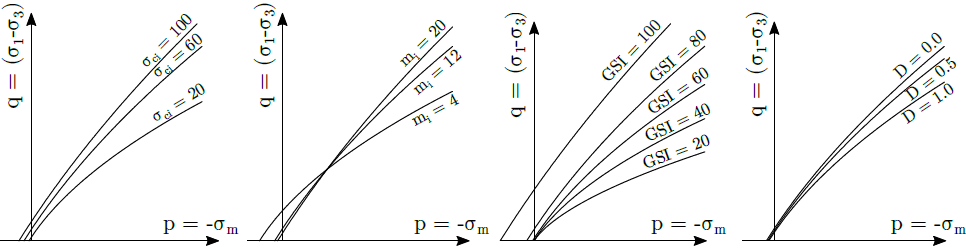
O impacto de cada parâmetro na projeção da superfície de cedência no plano meridiano é ilustrado na figura seguinte.
O modelo de Hoek-Brown implica a introdução do módulo de elasticidade do maciço rochoso Erm, que considera o estado de conservação do maciço rochoso. Pode ser determinado, por exemplo, com recurso aos parâmetros GSI, D e σci [2]
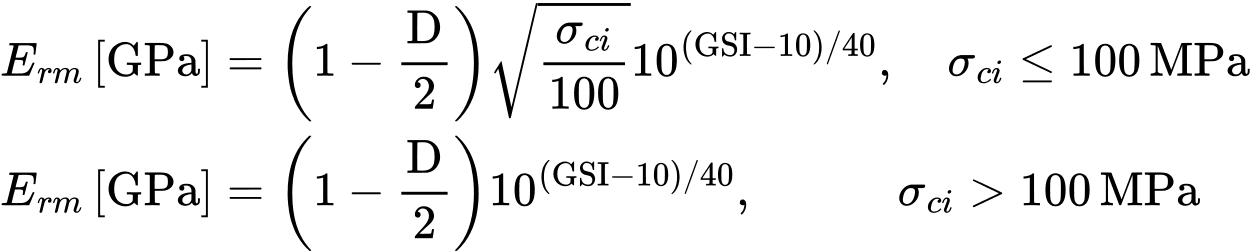
Estão disponíveis mais opções em [3].
O parâmetro a que ajusta a definição da relação na superfície de cedência também pode ser determinado através do the geological strength index GSI, de acordo com
A tabela seguinte apresenta os parâmetros do modelo.
Símbolo | Unidade | Descrição | |
| [MPa] | Módulo de elasticidade do maciço rochoso | |
| [-] | Coeficiente de Poisson | |
| [MPa] | Resistência à compressão uniaxial | |
| [-] | Constante de Hoek-Brown | |
GSI | [-] | Geological strength index | |
D | [-] | Fator de distúrbio | |
| [°] | Ângulo de dilatação ( o valor inicial | |
| [kN/m3] | Peso volúmico | |
| [-] | Constante de Hoek-Brown reduzida (definida ou calculada a partir de GSI, D, | |
| [-] | Constante material (definida ou calculada a partir de GSI, D) | |
| [kPa] | Resistência à tração máxima permitida, | |
TsRF | [-] | Fator de redução da resistência à tração (0,1), caso definida por | |
| [kPa] | Valor limite da pressão confinada para modelar a dilatação | |
| [1/K] | Coeficiente de dilatação térmica (quando são considerados efeitos de temperatura) |
é definido de acordo com a figura)
)
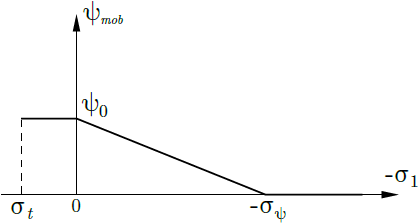
A condição é semelhante aos modelos de Drucker-Prager e de Mohr-Coulomb. Assim, é possível modelar a dilatação (desenvolvimento de deformações plásticas volumétricas durante o cisalhamento plástico) ao introduzir o ângulo de dilatação ψ. No entanto, o ângulo de dilatação não é necessariamente constante e pode evoluir conforme mostra a figura seguinte.
A implementação do modelo de Hoek-Brown introduz automaticamente o valor máximo da resistência à tração 
. Este valor pode ser definido ou calculado com base no fator de redução da resistência à tração TsRF, conforme a tabela com os parâmetros do modelo. De forma semelhante ao modelo de Mohr-Coulomb, a limitação da resistência à tração é dada pela superfície de cedência de Rankin.
O modelo de Hoek-Brown permite realizar a análise de estabilidade. Podem ser realizadas análises de estabilidade de taludes padrão como análises de estabilidade para etapas de construção específicas. No entanto, contrariamente ao modelo de Mohr-Coulomb, o modelo de Hoek-Brown considera o parâmetro η para reduzir a resistência à compressão uniaxial σci. Este parâmetro é descrito de acordo com o parâmetro de redução ζ, que reduz, por sua vez, os parâmetros de resistência ao cisalhamento c, φ, em modelos do tipo de Mohr-Coulomb. Pode encontrar mais detalhes no manual teórico.
A analogia com o modelo de Mohr-Coulomb está descrita com detalhe aqui. A resposta da modelo de Hoek-Brown em comparação com o modelo de Mohr-Coulomb está ilustrada no manual teórico, através da simulação de um ensaio laboratorial simples.
A implementação do modelo material de Hoek-Brown no programa GEO5 MEF está descrito em detalhe no manual teórico. Pode encontrar mais detalhes na bibliografia.
Bibliografia:
[1] E. Hoek and E.T. Brown, Practical estimates of rock mass strength, International Journal of Rock Mechanics and Mining Sciences, 34.8 (1997), 1165-1186
[2] E. Hoek, C. Carranza-Torres and B. Corkum, Hoek-Brown failure criterion - 2002 edition, Proceedings of the 5th North American symposium - NARMS-TAC (2002)
[3] E. Hoek, M.S Diederichs, Empirical estimation of rock mass modulus, International Journal of Rock Mechanics \& Mining Sciences, 43 (2006), 203-215