Módulo Edométrico
Se os resultados do ensaio edométrico estiverem representados através da curva edométrica (Δε = f(Δσef )), torna-se evidente que para cada ponto da curva existe um rácio σef /ε diferente.
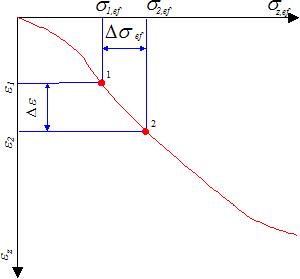 Determinação do módulo edométrico Eoed
Determinação do módulo edométrico Eoed
Se a curva tensão-deformação para um certo intervalo de duas tensões vizinhas σ1ef - σ2ef for substituída por uma linha secante, é aceitável assumir um comportamento do solo linear, dentro deste intervalo, e representar a compressibilidade do solo como Δσef/Δε - denominado módulo edométrico de deformação. O módulo edométrico de deformação é o módulo secante ligado a um dado intervalo de tensões σ1ef - σ2ef selecionado a partir do diagrama tensão-deformação Δε = (Δσef):
![]()
Em geral, o módulo edométrico de deformação Eoed tende a diminuir com o aumento do valor do intervalo de intensões. É necessário considerar, para cada camada, uma valor específico de Eoed, adequado a cada intervalo de tensões (do estado de tensão original ao final). Isto é considerado pelo programa através da forma de introdução de Eoed, onde é possível especificar, para cada solo, a curva edométrica respetiva (diagrama σef/ε).
No entanto, a partir da experiência prática sugere-se (para argilas, por exemplo) diferentes ordens de grandeza entre o valor de Eoed derivado a partir do módulo de deformação Edef e que é obtido a partir da medição in situ da curva de carga.
A relação entre Edef e Eoed é dada por:
![]()
![]()
onde: | ν | - | coeficiente de Poisson |
Edef | - | módulo de deformação |
Intervalo de valores aproximado para módulos edométricos de deformação Eoed para cada solo e intervalos de tensão típicos (prof. I. Vanicek: Soil mechanics):
Solo | Módulo edométrico Eoed [MPa] |
cascalhos | 60 - 600 |
areias mediamente densas a areias densas | 7 - 130 |
coesivo | 2 - 30 |
Bibliografia:
Vanicek, I.: Geomechanika 10: mechanika zemin. 3th edition, Prague, CTU, 2000, 229 s., ISBN 80-01-01437-1.